二分查找

本文最后更新于：6 个月前

二分查找是计算机科学中一种基本而强大的算法，它允许在对数时间内快速查找有序集合中的元素。这种方法通过不断将搜索区间分成两半来快速定位目标值，广泛应用于算法竞赛和软件开发中，接下来本文将对二分查找进行详细的介绍。

概念

二分查找（Binary Search），也称为折半查找，是一种在有序数组中查找某一特定元素的搜索算法。

术语

  • 目标target：要查找的值。
  • 索引index：查找的当前位置。
  • 左右指示符left、right：维持查找空间的指标。
  • 中间指示符mid：用来应用条件以确定向左查找还是向右查找的索引。

算法思想

通过不断将待查找的数据范围分成两半，然后根据中间值与目标值的比较，决定下一步在哪一半中继续查找，由于每次都能将搜索范围缩小一半，所以能加快搜索速度。

基本步骤

  1. 初始化：设定两个指针，一个指向数组的起始位置（left），另一个指向数组的结束位置（right）。
  2. 中间元素比较：计算中间位置的索引 mid = left + (right - left) / 2，并比较中间元素与目标值：
    • 如果中间元素等于目标值，搜索结束，返回该位置的索引。
    • 如果中间元素小于目标值，说明目标值位于数组的后半段，调整 left 指针到 mid + 1。
    • 如果中间元素大于目标值，说明目标值位于数组的前半段，调整 right 指针到 mid - 1。
  3. 迭代或递归：重复上述步骤，每次都根据比较结果调整查找范围，直到 left 指针超过 right 指针，这时如果仍未找到目标值，则表示数组中不存在该元素，返回 -1 或其他标识未找到的结果。

复杂度分析

  • 时间复杂度：O(log n)，因为每次查找都将查找范围缩小为原来的一半。
  • 空间复杂度：O(1)，只使用了常数空间。

特点

  • 高效：二分查找的时间复杂度为 O(log n)，其中 n 是数组的长度。相较于线性查找的 O(n)，二分查找在大数据集上表现更优。
  • 前提条件：二分查找要求数据结构是有序的。对于无序数据集，必须先进行排序，这可能会增加额外的时间成本。
  • 适用场景：最适合用于不经常变动但频繁搜索的数据集。例如，数据库的索引通常就是利用类似二分查找的算法进行优化的。

模板

用以下这道标准的二分查找为例，根据指针边界的定义（即区间的开闭情况），可分为4个模板。

704. 二分查找 - 力扣（LeetCode）

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

Ⅰ 左闭右闭

搜索区间包含左右边界，即[left, right]，适用于大多数基本的二分查找问题，其中目标值可能刚好位于数组的端点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int search(int[] nums, int target) {
        // 初始化左指针为0
        int left = 0;
        // 初始化右指针为数组长度减1
        int right = nums.length - 1;
        // 当处于合法区间（左指针不大于右指针）时，继续循环
        while (left <= right) {
            // 计算中间位置
            int mid = left + (right - left) / 2;
            // 如果中间元素大于目标值，则将新的二分查找范围缩减为mid的左区间
            if (nums[mid] > target) {
                // mid已经明确不符合条件，为了满足新区间的右闭，所以新区间取值为[left, mid - 1]
                right = mid - 1;
            }
            // 如果中间元素小于目标值，则将新的二分查找范围缩减为mid右区间
            else if (nums[mid] < target) {
                // mid已经明确不符合条件，为了满足新区间的左闭，所以新区间取值为[mid + 1, right]
                left = mid + 1;
            }
            // 如果中间元素等于目标值, 则返回中间位置，即找到目标值
            else {
                return mid;
            }
        }
        // 未找到目标值，返回-1
        return -1;
    }
}

Ⅱ 左闭右开

搜索区间包括左边界但不包括右边界，即[left, right)，常见于某些编程语言的标准库实现中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                // mid已经明确不符合条件，为了满足新区间的右开，所以新区间取值为[left, mid)
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

Ⅲ 左开右闭

搜索区间不包括左边界但包括右边界，即(left, right]，比较少见，但可能适用于某些需要初始边界外扩展的特定算法设计，如处理某些周期性边界问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int search3(int[] nums, int target) {
        int left = -1;
        int right = nums.length - 1;
        while (left + 1 <= right) {
            // 注意此处 +1 处理：mid的计算方式向右收缩更加积极，规避程序除法向下取整导致无法缩小范围的死循环
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                // mid已经明确不符合条件，为了满足新区间的左开，所以新区间取值为(mid, right]
                left = mid;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

Ⅳ 左开右开

搜索区间既不包括左边界也不包括右边界，即(left, right)，较少使用，适合于需要频繁调整边界判定逻辑的复杂查找或特殊情况处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int search(int[] nums, int target) {
        int left = -1;
        int right = nums.length;
        while (left + 1 < right) {
            // mid已经明确不符合条件，且为了满足新区间的左开右开，因此新区间取值为(left, mid)或(mid, right)
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

题型

标准二分

题目

35. 搜索插入位置 - 力扣（LeetCode）

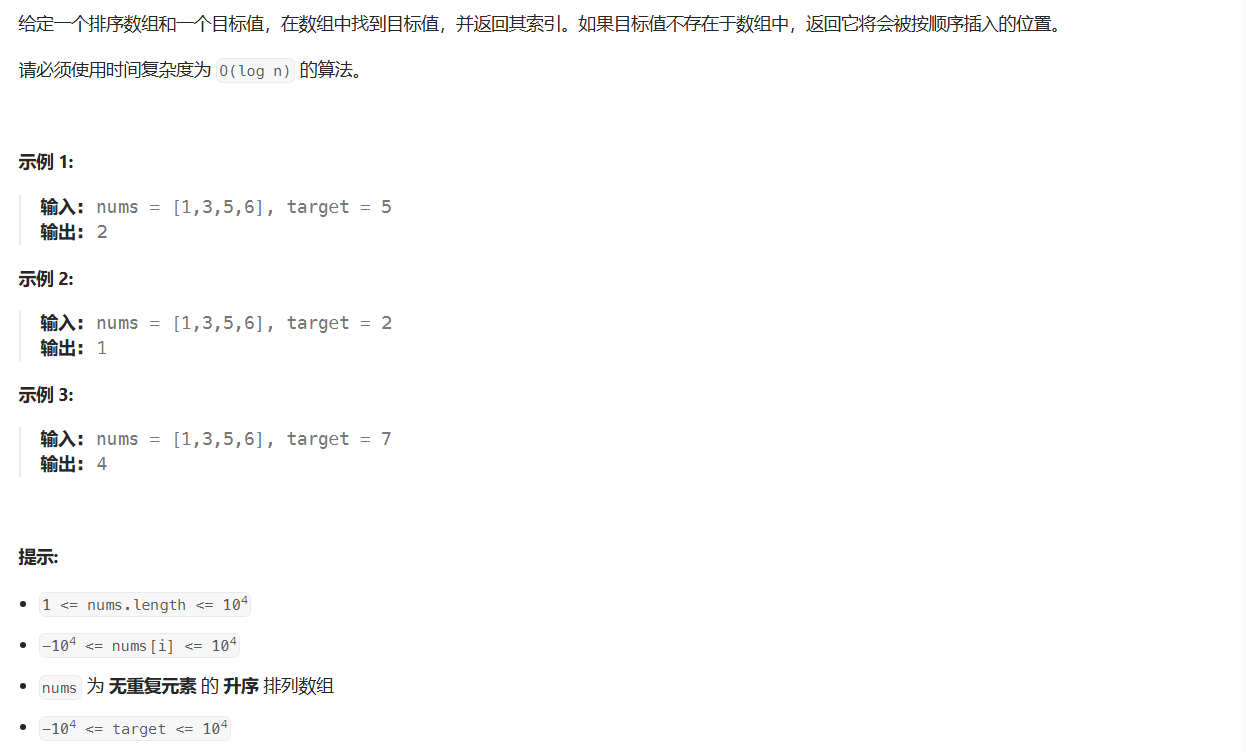
思路

这个问题是典型的二分查找应用。给定一个无重复元素的升序数组和一个目标值，需要找到目标值在数组中的索引或者应该插入的位置。二分查找是解决这类问题的理想方法，因为它能够在对数时间内缩小搜索范围。

解题过程

  1. 初始化指针：设置两个指针 left 和 right 分别指向数组的开始和结束位置。
  2. 二分搜索：计算中点 mid 并比较 nums[mid] 和 target：
    1. 如果 nums[mid] 等于 target，直接返回 mid 作为答案。
    2. 如果 nums[mid] 大于 target，调整 right 指针到 mid - 1，因为目标值在左半边。
    3. 如果 nums[mid] 小于 target，调整 left 指针到 mid + 1，因为目标值在右半边。
  3. 找到插入位置：如果循环结束还没有找到目标值，left 指针将指向应该插入目标值的位置。因为循环终止时，left 是第一个大于 target 的位置的索引。

复杂度

  • 时间复杂度：O(logn)，其中 n 是数组 nums 的长度。二分查找确保了对数级的搜索时间。
  • 空间复杂度：O(1)，只使用了有限的额外空间。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return left;  // left 是第一个大于 target 的位置
    }
}

数组中查找

题目

436. 寻找右区间 - 力扣（LeetCode）

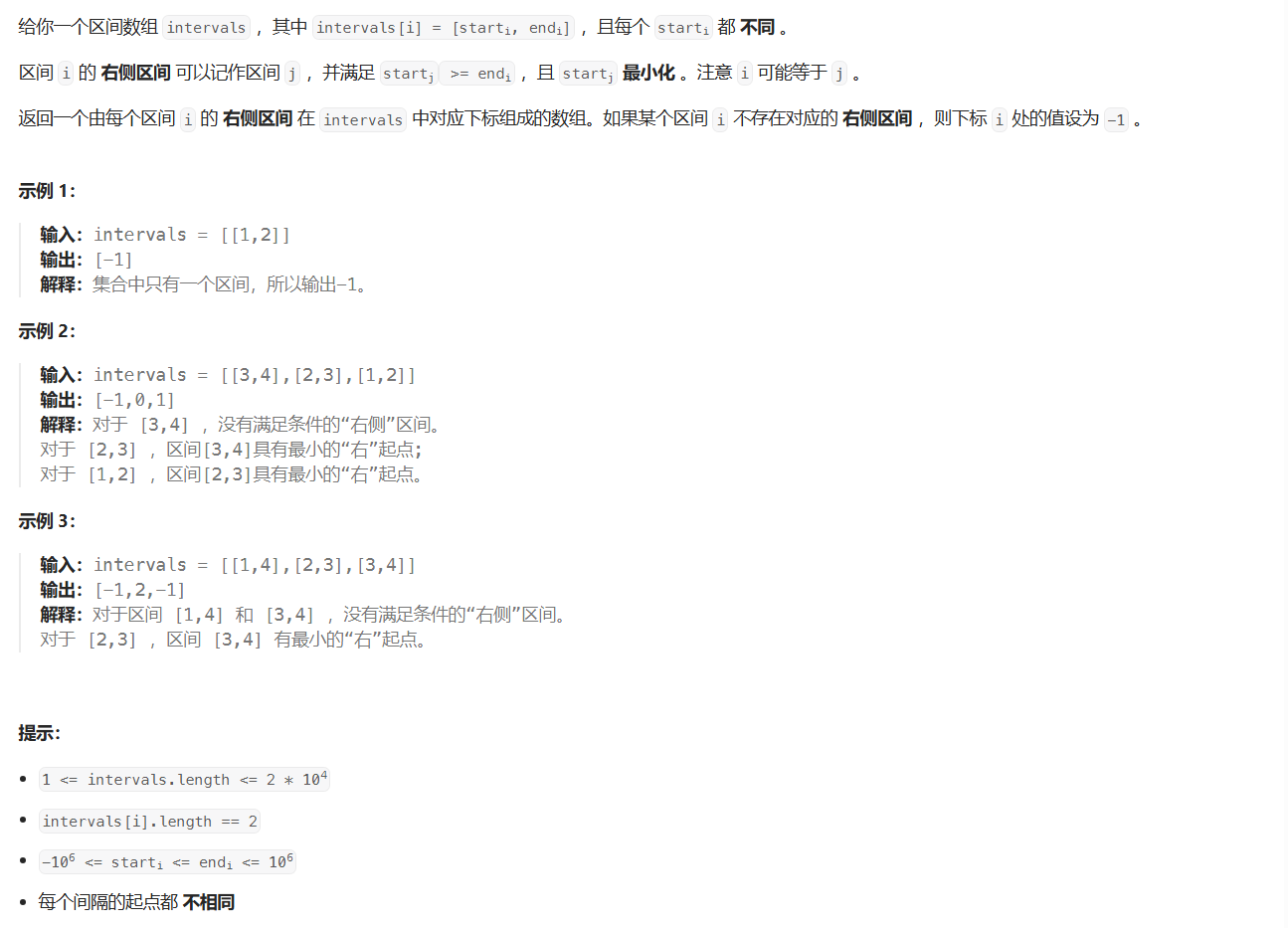
思路

解决这个问题的关键是能够快速找到每个区间的右侧区间。为了实现这一点，可以利用数组的排序和二分搜索。首先，我们需要对区间按起始位置进行排序。然后，对每个区间使用二分搜索来找到第一个起始位置不小于该区间结束位置的其他区间的索引值。

解题过程

  1. 构建辅助数组：创建一个数组 arr 来保存原始区间的索引和起始位置。这样在排序后我们仍能追踪到每个区间的原始位置。
  2. 排序：对 arr 按照区间的起始位置进行排序。排序后，对于任意区间 i，所有在 i 之后的区间都有不小于 i 的起始位置。
  3. 二分搜索：对于排序后的每个区间，使用二分搜索在 arr 中找到第一个起始位置大于等于该区间结束位置的区间。这个区间就是所求的右侧区间。
  4. 特殊处理：处理没有右侧区间的情况，即如果二分搜索没有找到符合条件的区间，则为该区间返回 -1。

复杂度

  • 时间复杂度：O(nlogn)，主要由排序和对每个区间进行二分搜索的操作组成，每次二分搜索的时间复杂度为 O(log n)，总共需要进行 n 次。
  • 空间复杂度：O(n)，用于存储辅助数组 arr 以及最终的答案数组。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] findRightInterval(int[][] intervals) {
        int l = intervals.length;
        int[][] arr = new int[l][3];
        for (int i = 0; i < l; i++) {
            // 保存原始索引
            arr[i][0] = i;
            arr[i][1] = intervals[i][0];
            arr[i][2] = intervals[i][1];
        }
        Arrays.sort(arr, (o1, o2) -> o1[1] - o2[1]);
        int[] ans = new int[l];
        for (int i = 0; i < l; i++) {
            // 在arr中查找第一个满足intervals[i][1]<arr[?][1]的arr[?][0]
            ans[i] = binarySearch(arr, intervals[i][1]);
        }
        return ans;
    }

    public int binarySearch(int[][] arr, int target) {
        int left = 0, right = arr.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (arr[mid][1] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left == arr.length ? -1 : arr[left][0];
    }
}

旋转数组

题目

33. 搜索旋转排序数组 - 力扣（LeetCode）

思路

此题要求在一个旋转排序数组中寻找目标值的索引。由于数组原本是升序的，但在某个未知下标上进行了旋转，使得该问题的解决需要考虑旋转的影响。该问题可以通过二分查找的方式解决，首先确定旋转点，然后在适当的半边数组中进行标准的二分查找。

解题过程

  1. 寻找旋转点：旋转点是数组中唯一的点，它比其右侧的元素大。通过二分查找来寻找这个点。此过程中，如果中间元素大于数组最右端的元素，旋转点必定在中间元素的右侧；否则，旋转点在左侧或就是中间元素本身。
  2. 判断搜索区域：确定旋转点后，需要判断目标值位于旋转点的左侧还是右侧。如果目标值在旋转点的值和数组最右端值之间，应在旋转点右侧搜索；否则，在左侧搜索。
  3. 执行二分查找：在确定的区域内执行标准的二分查找。如果找到目标值，返回其索引；否则，返回 -1 表示目标值不存在。

复杂度

  • 时间复杂度：O(logn)，这里 n 是数组的长度。整个过程中，寻找旋转点和在一半的数组中查找目标值都是通过二分查找实现的，每个操作的时间复杂度都是 O(log n)。
  • 空间复杂度：O(1)，只使用了常数个额外空间用于存储变量。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        int revIdx = findRevIdx(nums);
        if (nums[revIdx] == target) {
            return revIdx;
        }
        if (nums[right] >= target) {
            return bs(revIdx + 1, right, nums, target);
        } else {
            return bs(left, revIdx - 1, nums, target);
        }
    }

    // 二分查找返回下标
    private int bs(int left, int right, int[] nums, int target) {
        if (left > right) {
            return -1;
        }
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            return bs(mid + 1, right, nums, target);
        } else {
            return bs(left, mid - 1, nums, target);
        }
    }

    // 寻找数组翻转下标
    private int findRevIdx(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }
}

数学

题目

69. x 的平方根 - 力扣（LeetCode）

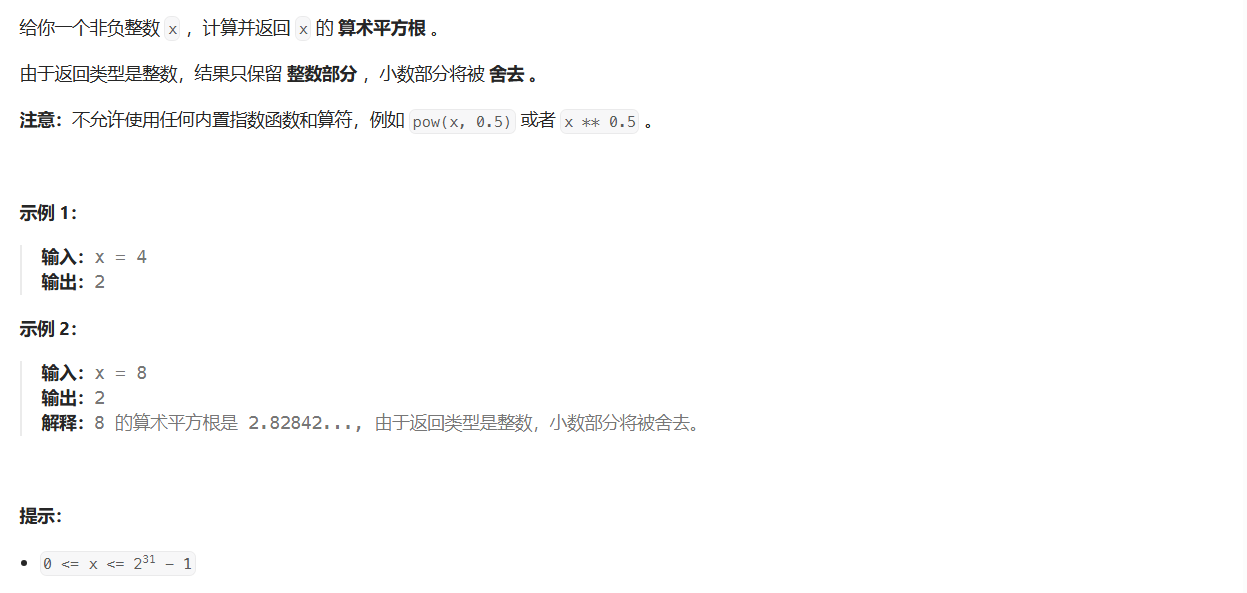
思路

计算整数 x 的算术平方根可以通过二分查找实现。问题的关键是找到一个数 m，使得 m^2 最接近且不大于 x。根据题意 x 的取值不会大于 2^31 - 1，可知结果的范围不会超过 2^16，我们可以在 0 到这个数的范围内使用二分查找来寻找这个数。

解题过程

  1. 初始化二分查找边界：left 初始化为 0，right 初始化为 65535，或者一个足够大的数（例如 65536，对于本题足够覆盖输入范围内的平方根）。
  2. 二分查找：在每次迭代中，计算 mid 作为 left 和 right 的平均值 mid，进而计算 mid 的平方 res。为避免整型溢出，使用 long 类型进行计算。
    1. 如果 res 小于 x，则 mid 可能是答案，但需要尝试更大的数，所以将 left 设置为 mid。
    2. 如果 res 大于 x，说明 mid 太大，需要尝试更小的数，所以将 right 设置为 mid。
    3. 如果 res 等于 x，直接返回 mid 作为答案。
  3. 返回结果：如果循环结束还没有找到恰好等于 x 的平方根，返回 left。这是因为当 left + 1 等于 right 时，已经确认 left 是小于等于 x 平方根的最大整数。

复杂度

  • 时间复杂度：O(logx)，二分查找的时间复杂度为对数级。
  • 空间复杂度：O(1)，仅使用了固定的额外空间。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int mySqrt(int x) {
        long left = 0;
        long right = 65536;
        while (left + 1 < right) {
            long mid = left + (right - left) / 2;
            long res = mid * mid;
            if (res < x) {
                left = mid;
            } else if (res > x) {
                right = mid;
            } else {
                return (int) mid;
            }
        }
        return (int) left;
    }
}

不变量

题目

275. H 指数 II - 力扣（LeetCode）

思路

这道题目要求计算科研人员的 h 指数，h 指数的定义是至少有 h 篇论文分别被引用了至少 h 次。数组已经按照升序排列，因此我们可以利用二分搜索来加速查找过程。

解题过程

  1. 初始化：设定二分搜索的边界，left 为 0，right 为论文总数减一（length - 1）。
  2. 二分搜索：
    1. 计算中点 mid，以及中点论文的引用次数 midVal = citations[mid]。
    2. 根据 h 指数的定义，如果 midVal 大于等于从当前论文到数组末尾的论文数量（length - mid），这意味着至少有 length - mid 篇论文被引用了至少 midVal 次。这种情况下，我们尝试查看是否可以有更大的 h 指数，即向左移动 right 边界。
    3. 否则，向右移动 left 边界，尝试找到满足条件的较小论文集合。
  3. 更新结果：如果找到符合条件的 h 指数，更新 ans。

复杂度

  • 时间复杂度：O(logn)，这里 n 是数组 citations 的长度。使用二分查找来优化查找过程。
  • 空间复杂度：O(1)，算法只使用常数额外空间。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int hIndex(int[] citations) {
        int length = citations.length;
        int ans = 0;
        int left = 0;
        int right = length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            int midVal = citations[mid];
            if (midVal >= length - mid) {
                ans = length - mid;  // 更新潜在的 h 指数
                right = mid - 1;     // 尝试寻找一个更大的 h 指数
            } else {
                left = mid + 1;      // 寻找满足条件的更小的集合
            }
        }
        return ans;
    }
}

作为一种方法

题目

300. 最长递增子序列 - 力扣（LeetCode）

思路

为了使递增序列更长，我们要尽量让序列“增长地更慢”，即保证序列中的元素尽可能小，增加后续元素扩展序列的可能性。为此维护一个辅助数组 arr，其中 arr[i] 表示长度为 i+1 的所有递增子序列中末尾元素的最小值。这个方法保证了 arr 数组是单调递增的，使得可以通过二分搜索来优化查找和替换操作。

解题过程

  1. 初始化：创建一个数组 arr，用来存储在扫描过程中遇到的递增序列的最小可能末尾值。arrLength 记录 arr 的有效长度，即最长递增子序列的当前最大长度。
  2. 迭代更新，遍历原数组 nums，对于每个元素
    1. 如果当前元素 nums[i] 大于 arr 的最后一个元素，则将其添加到 arr 的末尾，因为它可以扩展当前最长的递增子序列。
    2. 如果 nums[i] 小于或等于 arr 的最后一个元素，则使用二分搜索找到第一个不小于 nums[i] 的元素在 arr 中的位置，并替换它。这样做是为了保持 arr 中元素尽可能小，增加后续元素扩展序列的可能性。
  3. 二分搜索：利用二分搜索优化查找和替换操作，确保 arr 中的元素是有序的。

复杂度

  • 时间复杂度：O(nlogn)，其中 n 是 nums 数组的长度。每个元素最多进行一次二分搜索，每次搜索的时间复杂度为 O(log n)。
  • 空间复杂度：O(n)，需要额外的空间来存储 arr 数组。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] arr = new int[nums.length];
        arr[0] = nums[0];
        int arrLength = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > arr[arrLength - 1]) {
                arr[arrLength] = nums[i];
                arrLength++;
            } else {
                int index = binarySearch(arr, 0, arrLength - 1, nums[i]);
                arr[index] = nums[i];
            }
        }
        return arrLength;
    }

    // 二分查找target应插入的位置或替换的位置
    private int binarySearch(int[] arr, int left, int right, int target) {
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
}

结合贪心

题目

410. 分割数组的最大值 - 力扣（LeetCode）

思路

此问题要求将一个非负整数数组分割成 k 个连续子数组，使得这些子数组中的最大和最小。为实现此目标，我们采用二分搜索与贪心算法的结合。二分搜索确定最大子数组和的可能最小值，而贪心算法用来验证在给定最大子数组和的约束下是否能有效地分割数组。

解题过程

  1. 确定二分搜索范围：
    1. 下界为数组中的最大值，因为任何有效的分割方式中，最大子数组的和不可能小于数组中的最大单个元素。
    2. 上界为所有数组元素的总和，因为在极端情况下，所有元素都可以在一个子数组中。
  2. 二分搜索：对上述范围进行二分搜索，寻找可以满足条件的最小可能的最大子数组和。
  3. 贪心验证：对于每个中间值（即二分搜索的当前中值），尝试使用该值作为最大子数组和来分割数组。如果能将数组分割成不超过 k 个这样的子数组，则该中值可行。

复杂度

  • 时间复杂度：O(nlogS)，其中 n 是数组的长度，S 是二分搜索的范围，即从 max(nums) 到 sum(nums)。
  • 空间复杂度：O(1)，仅使用了有限的额外空间。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int splitArray(int[] nums, int k) {
        int left = 0, right = 0;
        for (int num : nums) {
            right += num;
            if (num > left) {
                left = num; // 最大的一个元素是最小可能的最大子数组和的下界
            }
        }

        while (left < right) {
            int mid = left + (right - left) / 2;
            if (valid(nums, k, mid)) {
                right = mid; 	// 如果可以实现，尝试更小的值
            } else {
                left = mid + 1; // 如果不可以实现，尝试更大的值
            }
        }
        return left;
    }

    private boolean valid(int[] nums, int k, int maxSum) {
        int currentSum = 0;
        int count = 1; // 至少需要一个子数组
        for (int num : nums) {
            if (currentSum + num > maxSum) {
                count++;
                currentSum = num; // 重新开始一个新的子数组
                if (count > k) {
                    return false; // 如果子数组数量超过 k，则不满足条件
                }
            } else {
                currentSum += num;
            }
        }
        return true;
    }
}

结合动态规划

题目

1235. 规划兼职工作 - 力扣（LeetCode）

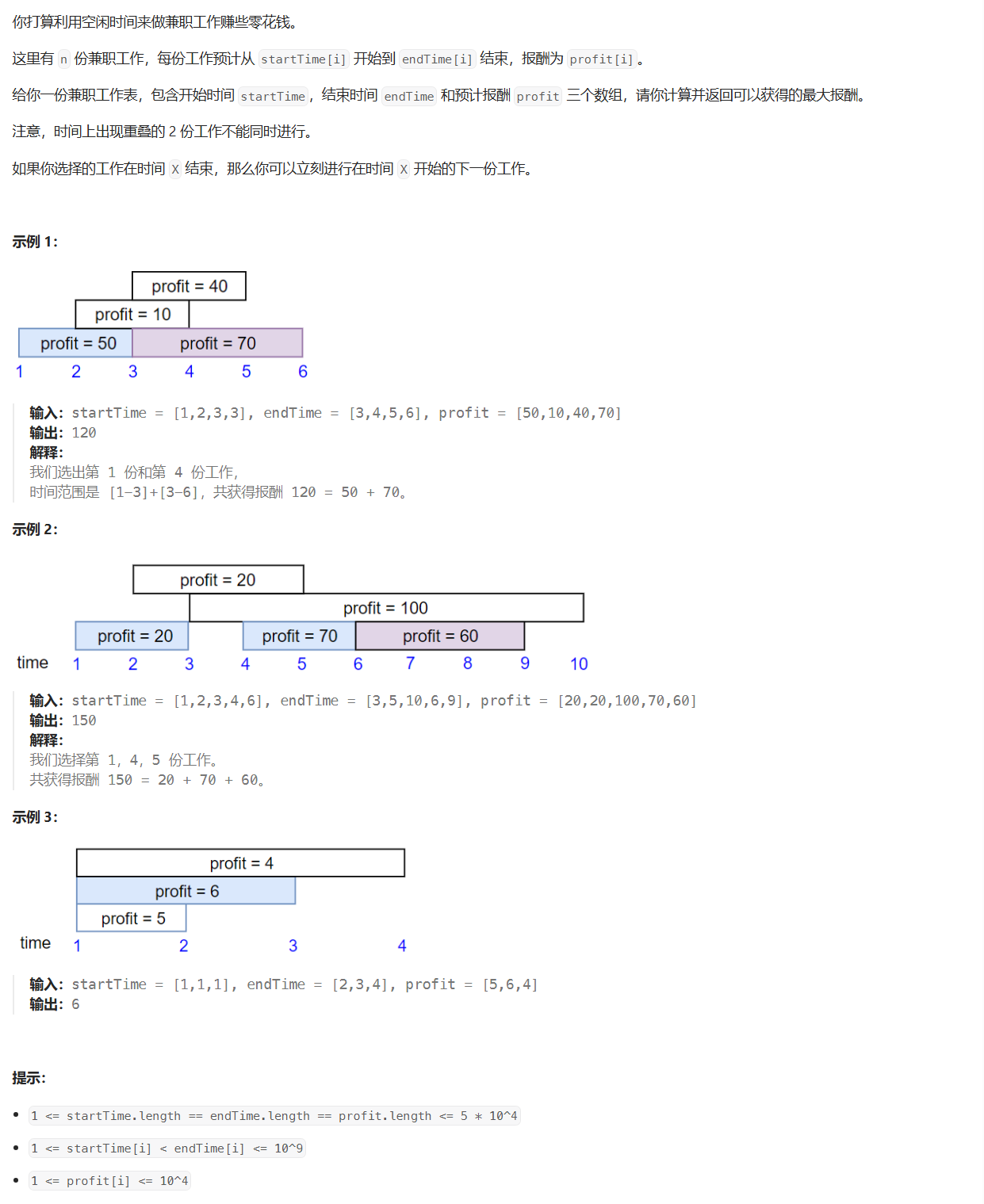
思路

这个问题要求解决的是一种典型的动态规划问题，结合了时间管理和最大化利润。任务是选择一系列不冲突的工作以获得最大收益。这可以通过排序和使用动态规划表来解决，其中利用二分搜索优化了寻找不冲突工作的过程。

解题过程

  1. 构造工作数组：将 startTime，endTime 和 profit 整合到一个数组 jobs 中，每个工作作为一个三元组 [开始时间, 结束时间, 利润]。
  2. 排序：按工作的结束时间对 jobs 进行排序。这样做可以更容易地管理工作之间的时间冲突。
  3. 动态规划初始化：创建一个动态规划数组 f，其中 f[i] 表示考虑到第 i 个工作时可以获得的最大利润。初始化 f[0] = 0。
  4. 填充动态规划表：
    1. 排序后的工作，对于每个工作，使用二分搜索找到最后一个结束时间不晚于当前工作开始时间的工作的索引 j。
    2. 更新 f[i] 为不选择当前工作时的最大利润 f[i-1] 与选择当前工作后的总利润 f[j + 1] + 当前工作的利润 中的较大值。
  5. 二分搜索实现：对于每个工作，查找不晚于该工作开始时间的最后一个工作的索引，这个索引用于确定不与当前工作冲突的前一个工作。

复杂度

  • 时间复杂度：O(nlogn)，其中 n 是工作的数量。排序需要 O(nlogn) 时间，每次插入动态规划表需要 O(logn) 时间进行二分搜索。
  • 空间复杂度：O(n)，用于存储排序后的工作和动态规划表。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int n = startTime.length;
        int[][] jobs = new int[n][];
        for (int i = 0; i < n; i++) {
            jobs[i] = new int[]{startTime[i], endTime[i], profit[i]};
        }
        Arrays.sort(jobs, Comparator.comparingInt(o -> o[1])); // 按照结束时间排序

        int[] f = new int[n + 1];
        for (int i = 0; i < n; i++) {
            int j = search(jobs, i, jobs[i][0]);
            f[i + 1] = Math.max(f[i], f[j + 1] + jobs[i][2]);
        }
        return f[n];
    }

    // 返回 endTime <= upper 的最大下标
    private int search(int[][] jobs, int right, int upper) {
        int left = -1;
        while (left + 1 < right) {
            int mid = (left + right) >>> 1;
            if (jobs[mid][1] <= upper) {
                left = mid;
            } else {
                right = mid;
            }
        }
        return left;
    }
}

总结

通过本文的学习，读者不仅可以掌握二分查找的基本方法和几种常见的变体，还可以通过实际的编程题加深理解和应用。掌握二分查找对于提高编程效率和解决复杂问题具有重要意义，是每个软件开发者必备的技能之一。

算法
算法 二分查找

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！